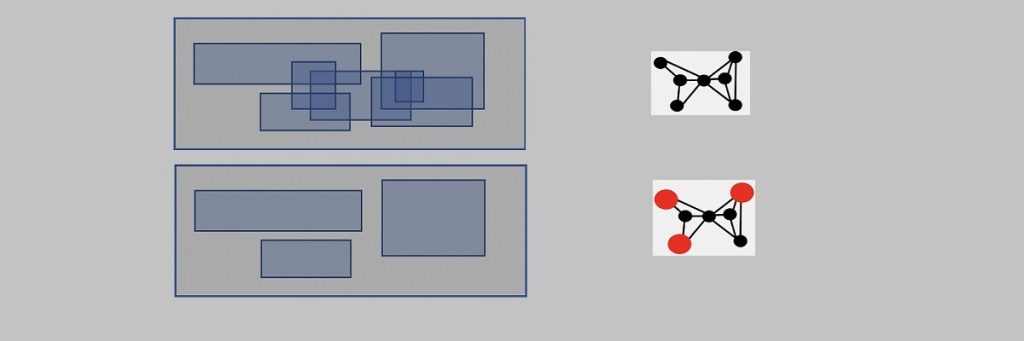
Maximum Independent Set of Rectangles (MISR) is a fundamental problem in fields such as computational geometry, approximation algorithms, and combinatorial optimisation. In this problem, given a set of (possibly overlapping) rectangles on a plane, one needs to find the maximum number of non-overlapping rectangles. MISR finds numerous applications in practice, such as in map labeling, data mining, and resource allocation. It also has rich connections with many important problems in theoretical computer science and discrete geometry. However, it is intractable to find the optimal solution for this problem. So, researchers are trying to find efficient and approximate solutions that are close to optimal.

Recently, Arindam Khan from the Department of Computer Science and Automation, undergraduate intern Madhusudhan Reddy, and international collaborators made progress on this notoriously hard problem by developing an algorithm that finds a solution that is at least one-third of the optimal solution.

In a follow-up study, they have further improved the result and showed an efficient algorithm that finds a solution (almost) half of the optimal solution. The work has led to the development of new mathematical techniques and extends the present techniques to their limits.