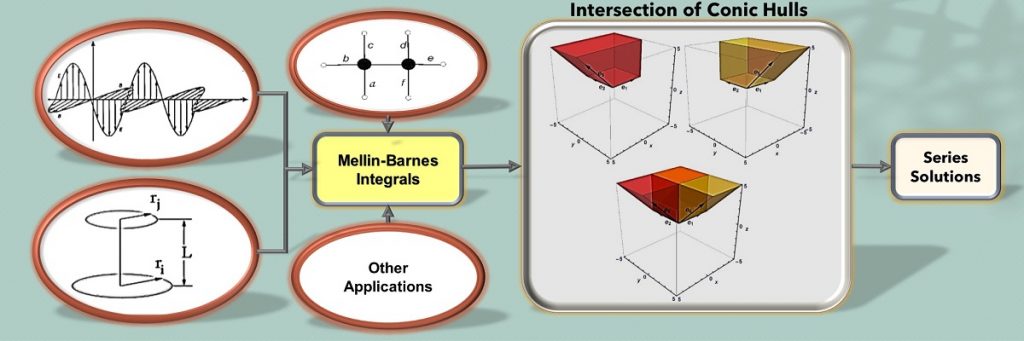
An important advance has been made towards the full solution of the old mathematical problem of constructing series representations of Mellin-Barnes (MB) integrals of arbitrary complexity. These are a special type of integral whose integrand consists primarily of ratios of products of Euler Gamma functions with complex number arguments.

MB integrals are ubiquitous in physics, engineering, and a variety of quantitative disciplines, and their evaluation ‒ particularly important for quantum field theory and hypergeometric functions theory ‒ has been an unsolved problem for over a century. In the present work, geometrical objects (conic hulls) and multivariate complex analysis have been combined in a new approach to make a breakthrough, allowing the researchers to evaluate MB integrals when the number of integrations is any fixed positive integer.

The technique is simple enough to be appreciated and applied by anyone with a firm grasp of high-school geometry. A computer package automating this method has also been produced by the authors, adding a powerful tool to the armoury of physicists and mathematicians. The study was carried out by B Ananthanarayan and Sumit Banik from the Centre for High Energy Physics, along with collaborators in Europe.