Investigating string theory led the scientists to a new series representation for the irrational number 

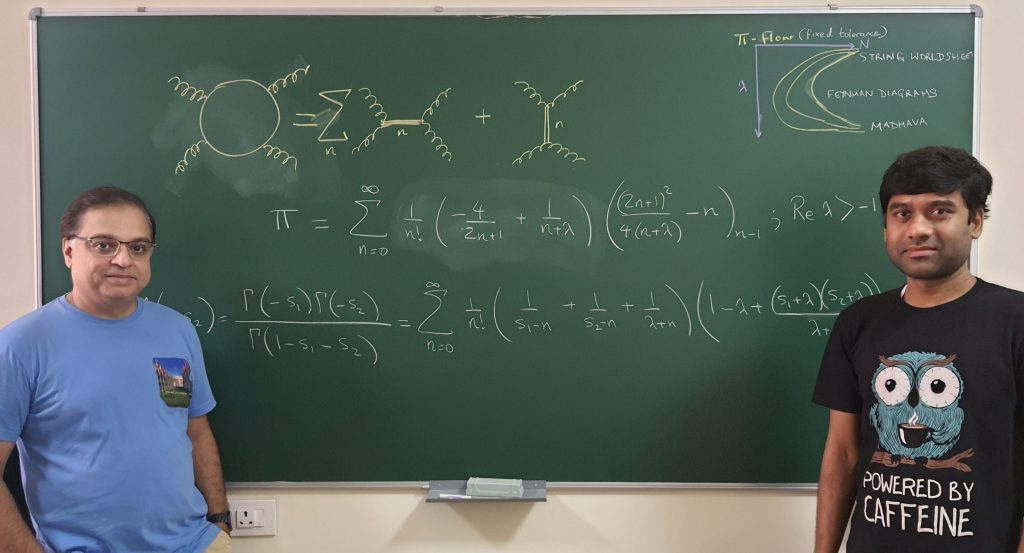
Aninda Sinha, a theoretical physicist at the Centre for High Energy Physics (CHEP), is interested in understanding in string theory – the theoretical framework that looks at physical phenomena and seeks to find a unified way to represent them by treating all processes in nature as simply different modes of vibrations plucked on a string.  

Sinha and his group at CHEP focus on how high energy particles interact with each other – such as protons smashing together in the Large Hadron Collider – and in what ways we can look at them using as few and as simple factors as possible. This way of representing complex interactions belongs to the category of “optimisation problems.” 

Arnab Saha, a post-doc who joined Sinha’s group, was keen on exploring this problem of optimisation. Like other physicists, Sinha and Saha turned to the language of physics: mathematics. They chose the well-known Euler Beta function, as it appears in the simplest scattering problem in string theory, and the Feynman diagram. Euler-Beta functions are mathematical functions used to solve problems in diverse areas of physics and engineering, including machine learning. The Feynman diagram is a mathematical representation that explains the energy exchange that happens while two particles interact and scatter. The idea was to understand how the scattering problem with the Euler-Beta representation would look like in terms of the Feynman diagram.  

What the team found was not only an efficient model that could explain features of string physics in quantum scattering, but also a series representation of pi, using rational coefficients and other parameters, such as irrational “cousins” called zeta functions.  

In mathematics, a series is used to represent a parameter such as pi in its component form. If pi is the “dish” then the series is the “recipe”. Pi can be represented as a combination of many numbers of parameters (or ingredients). Finding the correct number and combination of these parameters to reach close to the exact value of pi rapidly has been a challenge.  

The new formula under a certain limit closely reaches the representation of pi suggested by Indian mathematician Sangamagrama Madhava in the 15th century, which was the first ever series for pi recorded in history. 

“Although the new series representation does not provide the fastest representation for pi, the novel consideration used in this work leads to different physical pictures for the members of the family of these new representation, which include the Madhava series,” Sinha says. 

 The series or “formula” that Sinha and Saha stumbled upon combines specific parameters in such a way that scientists can arrive at the value of pi faster compared to the original Madhava series, and a similar strategy was incorporated in calculations involved in describing scattering of high-energy particles. 

Saha, who did the bulk of the calculations, admits that he was not expecting to get a series presentation for pi.  

“Physicists (and mathematicians) have missed this so far since they did not have the right tools which were only found through work we have been doing with collaborators over the last three years or so,” Sinha explains. “In the early 1970s, scientists briefly examined this line of research but quickly abandoned it since it was too complicated.” 

Many physical processes are inherently complex for many reasons, with many factors involved – like the collision of high energy particles in which the particles exchange energy and scatter in different directions. For instance, imagine a ball whose mass is negligible. Now, imagine that the ball is moving in a perfectly straight line with a sufficient speed. Thanks to Newton’s laws of motion, scientists have the right language to describe the state of the ball – where it is, and what speed the ball possesses at a given instant.  

To increase the complexity, imagine the same ball with a considerable mass, with the ball vibrating in addition to moving in a straight line. To describe the state of the ball, one might think we need a lot of math as the ball is not only moving forward but also vibrating in a different direction.  

Now imagine the ball is moving forward, vibrating, and spinning continuously. Then, imagine a spinning top in the place of a ball. The grammar of this physical process has now become much more complex. For such phenomena, many different factors influencing the motion of the object need to be taken into account – these factors or parameters are called degrees of freedom.  

As the degrees of freedom add on, the math required to explain a physical process becomes more complicated. This is why using math to represent processes like particle collision and scattering reaches very high levels of complexity. Sinha and Saha’s goal was to craft the right equations that would distill this complexity into something that would explain the behaviour of these scattering high-energy particles, especially at the quantum level, which falls under the purview of Quantum Field Theory (QFT).  

It was during such an effort that Sinha and Saha realised that their equations pointed to a new series representation (formula) for pi.  
 
Intrestingly, Sinha points out, when Paul Dirac published the mathematics of the motion and existence of electrons in 1928, he never thought that his findings would later provide clues to the discovery of the positron, and then to the design of Positron Emission Tomography (PET) used to scan our body for diseases and abnormalities.   

“Doing this kind of work, although it may not see an immediate application in daily life, gives the pure pleasure of doing theory for the sake of doing it,” Sinha adds.